- Associate Professor, Department of Information and Communications Engineering, Institute of Science Tokyo
- Research Interests: Quantum Error Correction, Coding Theory, Information Theory
Follow me on X
To realize useful quantum computation, it is essential to build a large number of reliable logical qubits. However, the current level of quantum computers is such that even with thousands of physical qubits, only a few tens of logical qubits can be obtained. While this limitation partly stems from engineering constraints such as device implementation and stability, even under an idealized setting of coding theory for quantum error correction, there remain fundamental challenges in code design itself.
Quantum Low-Density Parity-Check (LDPC) codes combined with low-complexity Belief Propagation (BP) decoding have long been regarded as a promising approach. Nevertheless, the following issues have persisted:
To date, no quantum error correction scheme has simultaneously overcome all of these obstacles.
By contrast, the field of classical error correction has already reached maturity. For instance, in mobile communications, LDPC codes have been adopted in the 5G standard, forming the backbone of real-world communication infrastructure. On personal computers as well, large-scale simulations with blocklengths up to \(10^7\) bits are feasible. While classical communication has achieved practical deployment of ultra-large-scale coding, quantum error correction codes are still far from reaching an equivalent level.
To address this situation, our research focuses on quantum error correction using LDPC codes, particularly the construction and decoding of Calderbank–Shor–Steane (CSS) quantum codes based on sparse binary or non-binary matrices. Our aim is to design quantum codes that approach the hashing bound under practical decoding algorithms.
One of our major achievements is the development of explicit quantum LDPC codes constructed from permutation matrices, which demonstrate excellent error-correcting performance over depolarizing channels. These constructions are carefully designed to avoid short cycles in the Tanner graph, thereby suppressing the error floor phenomenon.
We are also developing decoding algorithms that account for degeneracy in quantum noise models, including syndrome-based decoding and belief propagation methods adapted for Galois fields. Recent results indicate that combining dual codes with appropriate post-processing significantly improves the decoding success rate.
Through this line of work, we have attained performance close to the hashing bound, reduced error floors in low-rate regimes, constructed codes with large cycle lengths, and discovered binary LDPC codes with sharp error-rate transitions. This research contributes to the long-term goal of realizing scalable and fault-tolerant quantum communication and computation.
The software used in our recent publication (arXiv:2506.15636) is not yet fully prepared for public release, and the code is not well-polished. However, if that’s acceptable to you, it is available upon reasonable request.
The parity-check matrix data used in the paper is now available here: https://kasaikenta.github.io/2506.15636.code.tar.gz
The parity-check matrix data for our earlier work (arXiv:2504.17790) is also available here: https://kasaikenta.github.io/2504.17790.code.tar.gz
In the prefix_value files, the numbers 1, 2, ..., 255
represent \(\alpha^{0}, \alpha^{1}, \ldots, \alpha^{254}\) for a primitive element \(\alpha\).
The primitive polynomial can be found in the respective paper.
For other software or data related to the paper, please feel free to contact us.
The construction cleverly exploits two well-known insights from classical coding theory: (i) non-binary LDPC codes with column weight two tend to perform especially well under iterative decoding, and (ii) column weight two allows flexible designs that can effectively eliminate short cycles in the Tanner graph.
By combining these properties with affine permutation matrix (APM) placements, the proposed codes achieve both orthogonality and large girth, which suppress error floors and enable sharp threshold-like performance. As a result, the quantum LDPC codes constructed in this way approach the hashing bound, even at practical blocklengths.
The minimum distance of our codes does not grow linearly with blocklength. However, this does not prevent strong decoding performance under belief propagation (BP). From the theory of density evolution, it is well understood that what primarily determines BP performance are the column weight and row weight of the parity-check matrix, not the asymptotic growth of minimum distance.
Furthermore, it is known that classical LDPC codes with column weight three or larger typically have minimum distance that grows linearly with blocklength when constructed at random. This explains why researchers in LDPC coding theory tend not to emphasize minimum distance as the decisive factor: good iterative decoding performance can be achieved without relying on very large minimum distance.
While minimum distance is an important metric for characterizing the error-floor regime, achieving linearly growing minimum distance is not strictly necessary for excellent iterative decoding performance. This insight can be traced back to lessons from classical coding theory. During the 1980s and early 1990s, much of the community’s attention was directed toward the algebraic aspects of minimum-distance theory, and practical iterative methods received less focus. Consequently, the (re)discovery of turbo codes (1993) and LDPC codes (reintroduced in the mid-1990s, following Gallager’s original 1962 work) came somewhat later, even though their effectiveness derives not primarily from large minimum distance but from efficient iterative decoding and code structures that are well suited for BP.
Conventional quantum LDPC codes suffer from low coding rates, high error floors, lack of scalability, and heavy post-processing requirements. As a result, performance does not scale with blocklength and remains far from the hashing bound. Our work aims to construct codes with non-vanishing rate and efficient decoding that achieve performance close to the hashing bound.
The framework integrates four ingredients:
(i) Affine permutation matrix (APM) constructions to avoid short cycles,
(ii) joint belief propagation decoding over non-binary fields Fq,
(iii) optimization of minimum distance by carefully selecting matrix entries,
(iv) lightweight post-processing to remove residual errors.
Unlike conventional approaches that decode X and Z errors separately, our joint BP simultaneously estimates both, fully exploiting the CSS structure. Messages are richer because they are probability vectors over Fq rather than binary likelihoods, allowing more information to be exchanged during decoding. Residual trapping-cycle errors are corrected by local post-processing whose complexity is independent of code length.
Threshold phenomena and error-floor behavior become visible only at very large blocklengths. Demonstrating sharp threshold-like performance without error floors in this regime provides the strongest evidence of scalability. While short blocklengths also show good scaling, long blocklength results best highlight the theory.
The stabilizer weight is upper bounded by e × L, where e is the field extension degree and L is the row weight. For example, with e = 8 and L = 6, the stabilizer weight is at most 48, and crucially remains constant regardless of code length.
No. The analysis assumes an idealized setting where all gate operations, stabilizer measurements, and recovery operations are error-free. The purpose is to isolate the coding-theoretic limitations apart from engineering constraints.
No. Although matrices are defined over \( \mathbb{F}_q \) and decoding operates over non-binary fields, the physical system is still qubits. Each element of \( \mathbb{F}_q \) is expanded into an \( e \times e \) binary companion matrix, ensuring the code remains a binary CSS code.
Decoding is judged by whether the difference between the true error and the estimated error belongs to the dual code. In other words, if \( (x + \hat{x}) \in C_X^{\perp} \) and \( (z + \hat{z}) \in C_Z^{\perp} \), then the decoding is considered successful, because both correspond to valid stabilizers and represent the same logical state.
If the difference vector is not in the dual, then the estimated error introduces a logical error and decoding is considered unsuccessful. Our framework also includes lightweight post-processing that can correct many failures by resolving small trapping-cycle structures.
Our method generalizes the Hagiwara–Imai construction. Specifically, we place affine permutation matrices (APMs) at cyclically shifted positions within the parity-check matrices. By carefully choosing the shifts and the APM entries, the resulting non-binary matrices \( H_{\Gamma} \) and \( H_{\Delta} \) become orthogonal over \( \mathbb{F}_q \).
In other words, the inner product between any row of \( H_{\Gamma} \) and any row of \( H_{\Delta} \) cancels to zero in \( \mathbb{F}_q \). After expanding each field element into an \( e \times e \) binary companion matrix, we obtain binary parity-check matrices \( H_X \) and \( H_Z \) that satisfy \( H_X H_Z^{T} = 0 \). This approach ensures orthogonality while avoiding short cycles, leading to improved decoding performance.
In our framework, decoding success is not judged merely by reproducing the measured syndrome. Instead, the definition is stricter: the difference between the true error and the estimated error must belong to the dual code. In that case, the estimated error corresponds to a valid stabilizer and preserves the logical state, and only then is decoding counted as successful. If this condition is not met, the event is classified as a decoding failure since it introduces a logical error.
For further questions not covered here, please contact us directly via the Contact section below.
The paper titled "Quantum error correction near the coding theoretical bound", authored by Daiki Komoto and Kenta Kasai (Institute of Science Tokyo), has been published in npj Quantum Information.
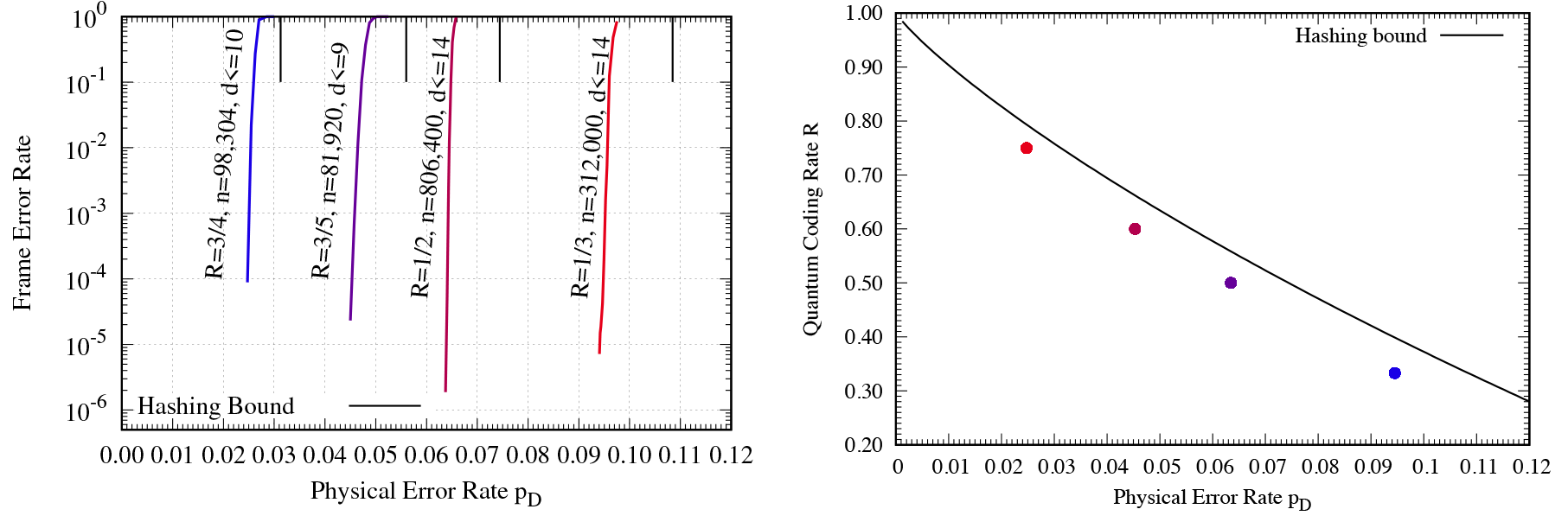
This study proposes a new quantum error correction framework based on LDPC codes that achieves performance near the coding-theoretical (hashing) bound. The work demonstrates efficient decoding for hundreds of thousands of logical qubits, marking a major step toward scalable fault-tolerant quantum computation.
We have released a new preprint titled "Sharp Error-Rate Transitions in Quantum QC-LDPC Codes under Joint BP Decoding" on arXiv.
This work reports the first observation of steep error-rate “waterfall” transitions in quantum LDPC codes with non-vanishing coding rate using binary joint belief propagation decoding. This phenomenon was previously believed to require more complex decoding strategies.
The paper also investigates the cause of error floors, identifying trapping sets in the Tanner graph as key contributors. These insights enable the potential design of codes and decoders that both maintain steep thresholds and reduce the error floor, moving quantum error correction closer to practical deployment.
Our new preprint titled "Quantum Error Correction Exploiting Degeneracy to Approach the Hashing Bound" is now available on arXiv.
This work presents a decoding algorithm that explicitly exploits the degeneracy of quantum errors under the depolarizing channel. Using non-binary LDPC codes and syndrome-based methods, the proposed decoder achieves a frame error rate of $10^{-4}$ at a physical error rate of 9.45% with a code of 104,000 logical qubits and 312,000 physical qubits, approaching the quantum hashing bound.
The following paper and poster presentations have been accepted to ISTC 2025 (13th International Symposium on Topics in Coding), which will be held in Los Angeles, USA, in August 2025.
The regular paper presents a novel construction of quantum APM-LDPC codes using non-circulant affine permutation matrices, demonstrating the feasibility of girth-16 code design beyond the conventional constraints of quantum QC-LDPC codes. The poster presentations provide an overview of recent developments in quantum error correction using non-binary LDPC codes and future directions for high-girth code constructions.
Prof. Kenta Kasai (Tokyo University of Science and Technology) will present his poster titled “Perspectives on Degeneracy and Structure in Non-Binary LDPC Code-Based QEC” at the ISIT 2025 workshop “Quantum Information – Open Problems, Impact, and Challenges (Q-PIC)”.
The workshop focuses on key challenges and open problems in quantum information science, and the poster highlights new perspectives on degeneracy and structural properties in quantum error correction based on non-binary LDPC codes.
The poster will be on display starting at 9:30 AM on June 24, 2025 (Tuesday) at the Rackham Graduate School, University of Michigan. Prof. Kasai will also deliver a 30-second pitch talk and be available for Q&A sessions.
For more details, please visit the Q-PIC workshop page.
Prof. Kenta Kasai (Institute of Science Tokyo) will present his recent work titled “Follow-Up Study on Efficient Mitigation of Error Floors in Quantum Error Correction using Non-Binary LDPC Codes” at the Recent Results Poster Session of the IEEE International Symposium on Information Theory (ISIT) 2025.
The session will take place on Monday, June 23, 2025, from 14:30 to 15:50 at the ballroom of the Michigan League in Ann Arbor.
This follow-up study builds upon previously proposed techniques to mitigate error floors in quantum LDPC codes and evaluates their performance and practicality in greater depth.
The poster "Towards Practical Quantum Error Correction: Near-Optimal Performance and Floor Mitigation via Non-Binary LDPC Codes", authored by Kenta Kasai, has been accepted for presentation at the Quantum Error Correction (QEC25) conference.
This work addresses the suppression of error floors in quantum LDPC codes and demonstrates near-optimal performance using non-binary belief propagation decoding.
The acceptance rate for this year’s poster session was below 40%, making it a highly competitive venue for recent results in quantum error correction.
More details available on the QEC25 website.
The paper "Efficient Mitigation of Error Floors in Quantum Error Correction using Non-Binary Low-Density Parity-Check Codes", authored by Kenta Kasai, has been accepted for presentation at the IEEE International Symposium on Information Theory (ISIT 2025).
This paper presents decoding algorithms designed to mitigate the error floor in quantum LDPC codes constructed over non-binary fields, achieving performance close to the hashing bound under practical quantum noise models.
As a follow-up to this work, we will present new results in the Recent Results Poster Session at ISIT 2025, to be held in Ann Arbor, Michigan.
Preprint available on arXiv.
Email: kenta@ict.eng.isct.ac.jp
Office: Room 418, South Building 3, Ookayama Campus, Institute of Science Tokyo
2-12-1, Ookayama, Meguro-ku, Tokyo 152-8550, Japan